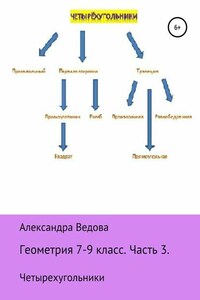
Геометрия 7-9 класс. Часть 4

О книге

Автор книги - Александра Ведова. Произведение относится к жанру учебная литература. Оно опубликовано в 2020 году. Книге не присвоен международный стандартный книжный номер.

Аннотация

Последняя четвертая часть книги по геометрии. В этой части мы собрали информацию о многоугольниках, окружности и круге. Цель книги – помочь школьникам и всем интересующимся планиметрией понять ее и запомнить. По разным причинам школьникам бывает тяжело усвоить всю информацию на уроках, еще тяжелее ее выучить, запомнить и понять перед экзаменом. В этой книге информация даётся блоками, что помогает лучше и быстрее усвоить нужный материал. Книга разделена на несколько частей для удобства.

Читать онлайн Александра Ведова - Геометрия 7-9 класс. Часть 4

От автора

Эта книга предназначена для обычных школьников, которые хотят понять геометрию на плоскости, но в силу разных обстоятельстве в школе им это не удалось сделать. Книга разделена на несколько частей: для удобства изучения и для качественного усвоения материала. Все части книги связаны и представляют собой единую программу по предмету Геометрия, раздел «Планиметрия».

Пусть наука простит меня за какие-то возможные неточности в изложении материала, я не для нее писала эту книгу и старалась максимально связно и доходчиво донести знания до детей любого возраста и для родителей, которые хотят помочь своим чадам в изучении этого предмета или вместе изучают предмет.

Программа отработана и показывает хорошие результаты усвояемости учениками разных возрастов, от 5 до 11 класса.

Планируется выпустить сначала все книги по теории, потом задачники.

Окружность и круг.

Окружность – это замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра).

Точка O – центр окружности.

Все точки окружности равно удалены от центра – это значит, что расстояние от центра до любой точки окружности одинаковое

, это расстояние называется радиуса.

Градусная мера дуги. Центральный угол.

Дуга – это часть окружности. Т.к. окружность измеряется в градусах, то и дуга также измеряется в градусах. В окружности , любое значение меньше, чем – это градусная мера душ.

На рисунке отмечены точки A и B. Эти точки делят окружность на две дуги AB. Чтобы их различать, на каждой отмечают промежуточную точку. AMB, ANB

Нарисуем окружность и проведем диаметр CK. Диаметр делит окружность на две полуокружности, т.е. пополам, значит дуги CK (CBK и CAK) являются полуокружностями и составляют

(целая окружность

значит

). Заметим, что COK – это развернутый угол, его градусная мера также составляет

Отсюда следует, что угол, проходящий через центр окружность (его называют центральный угол) и дуга имеют одинаковую меру.

Соответственно, чем меньше угол, тем меньше дуга. Чем больше угол, тем больше дуга. Градусная мера большего угла равна градусной мере большей дуги. Градусная мера меньшего угла равна градусной мере меньшего угла.

Взаимное расположение прямой и окружности

Рекомендации для вас